カーボンナノチューブのエネルギーバンド
カーボンナノチューブはグラフェンを円筒状に丸めた立体構造をしています。何重にもチューブが重なった多層カーボンナノチューブもありますが、ここでは、一層のチューブからなる単層カーボンナノチューブについて簡単に紹介します。エネルギーバンド計算の実行をお試し下さい。
カーボンナノチューブの立体構造
ナノチューブの立体構造は、グラフェンを丸める方向を表すカイラルベクトル \[ \overrightarrow{C}_h = n \overrightarrow{a}_1 + m \overrightarrow{a}_2 \equiv (n,m) \] によって指定されます。\( \overrightarrow{a}_1, \overrightarrow{a}_2 \)はグラフェンの基本格子ベクトルです。2つの整数の組 \( (n,m) \) はカイラリティと呼ばれ、これによりナノチューブの立体構造が指定されます。
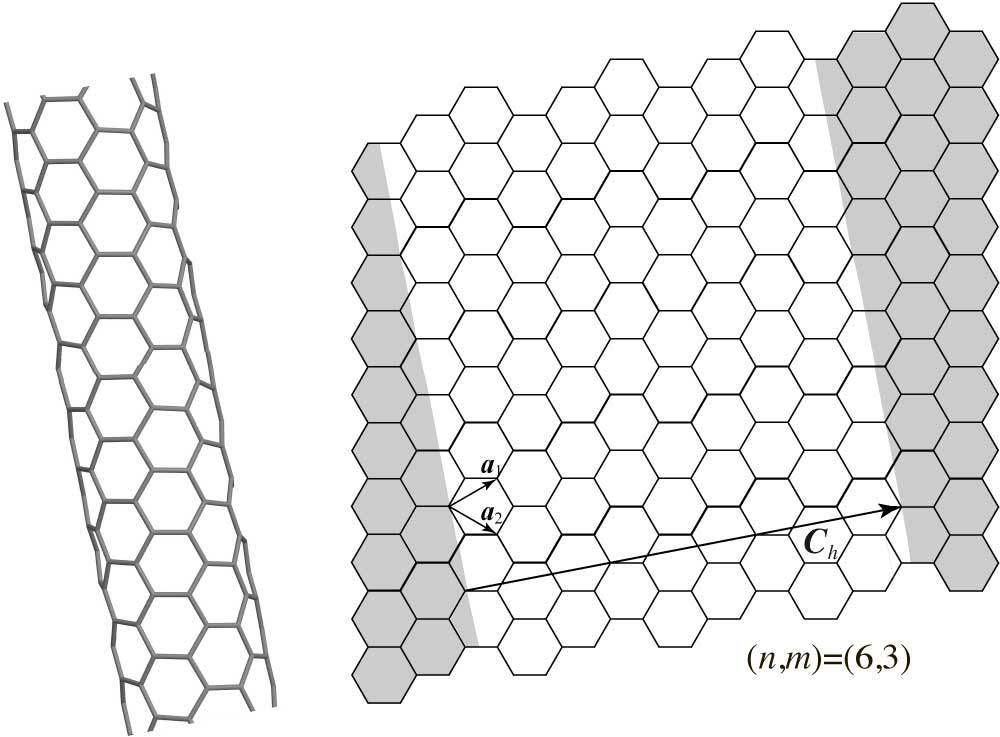
ナノチューブの立体構造とその展開図の模式図
金属、もしくは、半導体
カーボンナノチューブは、カイラリティによって金属もしくは半導体になることが知られています。それによると、 \( n - m \) を \( 3 \) で割ったときの余りがゼロだと金属、それ以外では半導体となります。この性質は、エネルギーバンドを計算することで確認することが出来ます。以下では、実際にエネルギーバンドを計算し、この性質を確認してみましょう。
補足事項:実際には、上記分類で金属とされるナノチューブにおいても、ナノチューブ表面の有限曲率の効果により、微小ギャップが存在することが知られています。
電子状態を計算するためのモデル
各原子に局在した電子軌道が隣り合う原子の原子軌道と混成する効果を取り入れたタイトバインディンディングモデルが知られています。ここでは各炭素原子のπ軌道のみを考慮したタイトバインディングモデルを取り扱います。さらには、ナノチューブの持つ対称性(軸周りの回転対称性)を利用して、モデルをより簡略化でき、計算の負荷を下げることも可能となります。以下のエネルギバンド計算では、この性質も利用しています。エネルギーバンドの計算
ここでは、カイラリティ \( ( n, m ) \) を指定し、上記で示したタイトバインディングモデルに対するエネルギーバンド計算を実行します。半導体の場合には、エネルギーバンドの価電子帯と伝導帯との間にeV程度のエネルギーギャップが存在する、一方、金属の場合には、ギャップが存在しない、といったことを確認できるかと思います。エネルギーバンド計算の縦軸の数値の単位はmeV(ミリ電子ボルト)です。
エネルギーバンド計算結果プロットの下に表示される図は、簡略化されたモデルの模式図(●が局在軌道、●を繋ぐ線が起動間の混成)を表します。
Used plot library: Plotly
参考文献
カーボンナノチューブの基本的な事柄について日本語で書かれた参考書として、以下などがあります。 ここで示したエネルギーバンドの計算に用いたモデルについては下記論文に詳細を記しています。- W. Izumida, R. Okuyama, R. Saito, Physical Review B, 91, 235442 (2015).
- W. Izumida, R. Okuyama, A. Yamakage, R. Saito, Physical Review B, 93, 195442 (2016).
- R. Okuyama, W. Izumida, M. Eto, Journal of the Physical Society of Japan, 86, 013702 (2017).
- Rin Okuyama, Wataru Izumida, Mikio Eto, Physical Review B, 99, 115409 (2019).