イジングモデル・シミュレータ

簡単に、イジングモデルとシミュレーション法を説明します。 厳密さを欠いた、ざっくりとした説明になること、ご容赦ください。 より詳しく知りたい方は、検索エンジンなどで調べてみてくださいね。 または、物理学科、物理学専攻への進学を検討して下さい。

イジングモデル

正方格子の格子点上にスピンが並び、各々のスピンは、 上向き、もしくは、 下向き、 の２方向を向くことができるとします。 隣り合ったスピンの間には互いに同じ方向を向くほうがエネルギー的に得をする、 という相互作用が働くものとします。
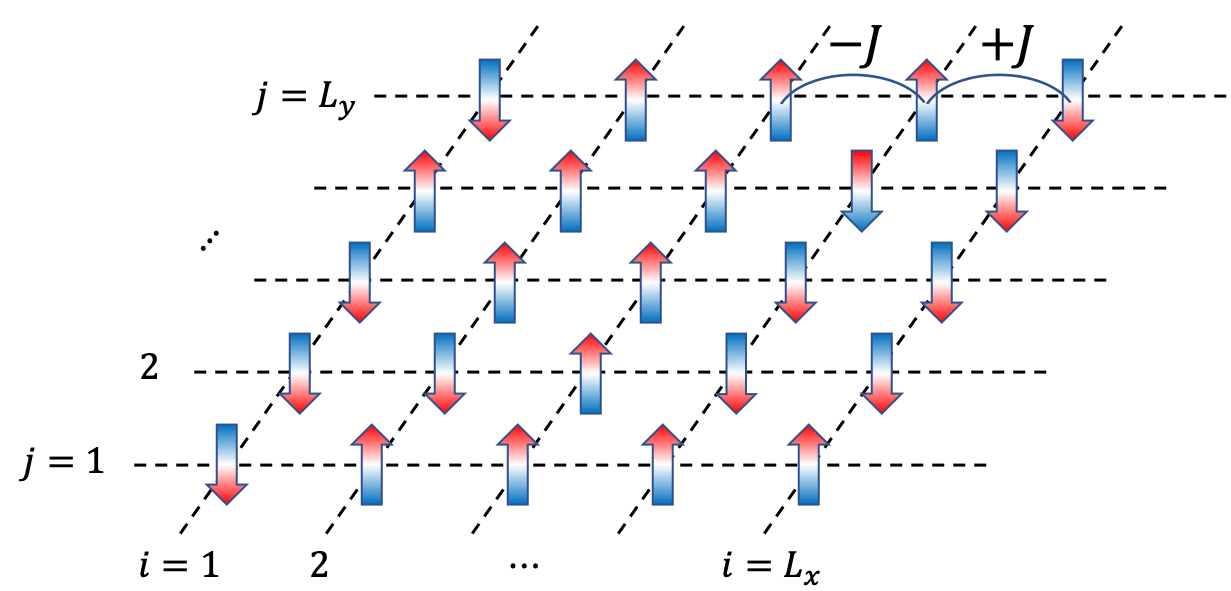
このモデルは、イジングモデルと呼ばれ、磁性体などの簡単な微視的モデルとして知られています。

系の状態とモンテカルロ法

系の状態（以下では多体状態もしくは単に状態と呼ぶ）は、 全ての格子点上のスピンの向きを定めることで指定されます。 統計力学によれば、絶対温度 \( T \) において 状態 \( \alpha \) が実現する確率は、 \[ P = \frac{1}{Z} \exp \left( - \frac{ E_{\alpha} }{k_B T} \right), ~~~~ Z = \sum_{\alpha} \exp \left( - \frac{ E_{\alpha} }{k_B T} \right). \] に従います。ここで \( k_B \) はボルツマン定数、 \( E_{\alpha} \) は状態が \( \alpha \) であるときの系のエネルギーです。
以下では、このような確率分布に従う多体状態を、 により数値的にシミュレーションします。 より具体的には、メトロポリス法と呼ばれるアルゴリズムを用いて、多体状態を生成していきます。 シミュレーション実行後十分に時間が経過すると、上記確率に従う状態が生成されると考えられています。

数値シミュレーション

パラメータを適当に選んで、モンテカルロ法によるシミュレーションを実行してみてください。
隣り合うスピン間の相互作用 \( J \) にくらべ温度が小さいとき（\( k_B T \ll J \)）、 大きいとき（\( k_B T \gg J \)） の違いを確認してみてください。 低温ではそれぞれのスピンが揃う傾向が、高温ではそれらスピンがバラバラの方向を向く様子が、 観られることと思います。
上向きスピンを赤丸、下向きスピンを青丸で表します。

\( T \) : K \( J \) : \( L_x \) : \( L_y \) :

---