はじめに

ある日、中学生の娘が「パパ、円周率ってどうやって求めるの？」と尋ねてきた。そのときは「円周率は円周の長さを直径で割るんだよな。」と答えるが、翌日も同じ質問。
よくよく聞くと、自分で実際に 円周と直径を測って計算してみても3.14...の数値が出てこなかったとのこと。 それに、いろんなところで見かける3.14159265...とずっと小数点以下の数字が並んでいき今では兆を超える桁数の結果がスーパーコンピュータを使って得られていることも知っているようだったが、 どうやってコンピュータで円周を測るの？など、確かにいろんな疑問が湧いてきますね。いつの間にか物わかりのいい大人になってしまっている自分に気付かされました．．．。
級数展開で求める、とかだと、そこまで行き着くまでの予備知識が結構必要だし．．．。 わかりやすいのは、円に外接、内接する正多角形で円を近似的に表すというのが中学生への説明としてはスタンダードな方法でしょうかね。 と言うわけで、この機会に少しまとめてみました。
これをきっかけにプログラミングに興味を持ってくれることを期待しつつ。

そういえば、小学生の頃そろばん塾に通っていましたが、8月8日はそろばんの日だそうで、その日に円周率がずらーっと書かれた下敷きをもらった覚えがあります。それを見て円周率をどのくらい覚えられるかを友達と競い合っていたなぁ。 数値計算の中で円周率を用いるときには、他の変数と精度をあわせるために、プログラム中で pi = 4 * atan(1.d0) などと定義してたなあ。
なんてことをを思い出しつつ。

円に内接・外接する正多角形の外周の長さ

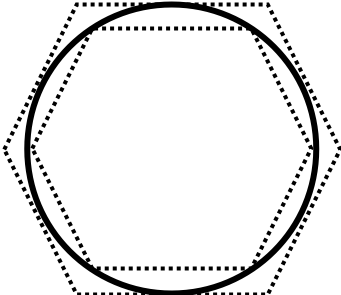
Circle, circumscribed and inscribed hexagons
直径1の円に図の様に外接、内接する正多角形（ここでは正\( 6 \times 2^n \)角形とします）の外周の長さをそれぞれ \( a_n, b_n \) とすると \begin{equation} b_n < \pi < a_n \end{equation} の関係があり、\( n \) を大きくすれば \(a_n, b_n\) はそれぞれ \( \pi \) に漸近するはずですね。 \(a_n, b_n\) は次の式で表されます。（ここでは導出しませんが、導出に挑戦してみましょう！） \begin{equation} a_{n+1} = \frac{2 a_n b_n}{a_n + b_n}, \quad b_{n+1} = \sqrt{ a_{n+1} b_n}. \end{equation} なお初項は \begin{equation} a_{0} = 2 \sqrt{3}, \quad b_{0} = 3, \end{equation} です。 この漸化式を用いて \( n=1 \) から順次求めれば良いわけですね。

実際に計算してみる

以下では、上記漸化式を計算するプログラム（はいろんな言語で作成できますが、ここではJavascriptを使用）を作りましたので、これでを用いて計算してみたいと思います。 （いくら\(n\)を大きくしても数値計算の精度の範囲までしか求まらないことに注意！）
n=： 外接する多角形の外周長： 内接する多角形の外周長：

（2019/07/27更新）

後記

この話をKさんにしたところ、
「以前、ゆとり教育で円周率が3と教えられている、っていうのが話題になってたよね。 そのころ、東大で「円周率が3.05より大きいことを証明せよ」という問題が出たんだよ。」
と教えてもらいました。いい問題ですね。 上記の考え方を使うと解けますね。
簡単にして、
「円周率が3より大きいことを示せ。」
なら小学校の学習内容の知識でいけるよね？
それに加えて
「円周率が \( 2 \sqrt{3} \) より小さいことを示せ。」
まで問うなら、中学生かな？ 娘に聞いてみよう。
（2020/01/28記）

Copyright © Wataru Izumida, All Rights Reserved.