1 + 1 with Quantum Computation
はじめに
量子ドットは電子やスピンを1個単位で制御できる点が大きな特徴として挙げられます。
量子的な性質に関する基礎研究の舞台としてだけでなく、
量子コンピュータの基本素子、すなわち一つ一つの量子ビットを操作することによる量子計算を実現するためのの基本素子、としての応用が期待されています。
このような性質を有する様々な微細系(半導体量子ドットやカーボンナノチューブなど)に対する物性研究が、私だけでなく、様々な研究グループによってすすめられてきました。
ここには、私が研究してきた系が今後量子ビットとして活用される際、それを具体的にどのように用いるのか、といった観点から、量子計算に関して簡単に記してみました。
量子コンピュータで1+1を計算する
いわゆる量子ゲート方式の量子コンピュータにおいて 1+1 をどのように計算するかについて簡単にまとめておきたいと思います。
ここで取り上げる例は、量子コンピュータが従来型のコンピュータに比べて有力であるとされる並列性を用いているわけではありませんが、計算の流れをつかむには良いように思います。
最後に、1+1に限らず \(q_1, q_2\)2ビットの加算を具体的に試すことができるようにしてみました。
4ビット系
ここでは4つの量子ビット \(q_1, q_2, q_3, q_4\) を用いる例を示します。
それぞれの量子ビットは \(q_n=0,1\) の2状態を取ります。
ここで説明する例は、\(q_1 + q_2\)の演算になります。
\(q_1\)と\(q_2\)に加算したい数値を指定します。
一方の他のビットは、入力時には\(q_3 = 0, q_4 = 0\)で、演算後これらは変更を受けます。
計算結果は\(q_3 q_4\)のように読みとります。
量子状態
系が取り得る状態数は \( 2^4 = 16\) あります。
よって、系の状態は16次元のベクトルで表すことが出来ます。
ベクトルの各成分は \(| q_1 q_2 q_3 q_4 \rangle \) 状態の係数を表すとします。
また、ベクトルの基底は
\[
| 0000 \rangle, | 0001 \rangle, | 0010 \rangle, | 0011 \rangle, | 0100 \rangle,
| 0101 \rangle, | 0110 \rangle, | 0111 \rangle, | 1000 \rangle, | 1001 \rangle,
| 1010 \rangle, | 1011 \rangle, | 1100 \rangle, | 1101 \rangle, | 1110 \rangle,
| 1111 \rangle
\]
の順に並ぶとします(2進数表記したときに0から数字が1ずつ大きくなっていく順)。
1+1の演算に対応する初期ビットは\( q_1 = 1, q_2 = 1, q_3 = 0, q_4 = 0 \)なので、
\(| 1100 \rangle\)状態のみが存在する、つまり初期状態に対応するベクトルは
\[
v_{\rm ini}^{T} =
\left(
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0
\right),
\]
と表されます。
量子演算を表すユニタリー変換
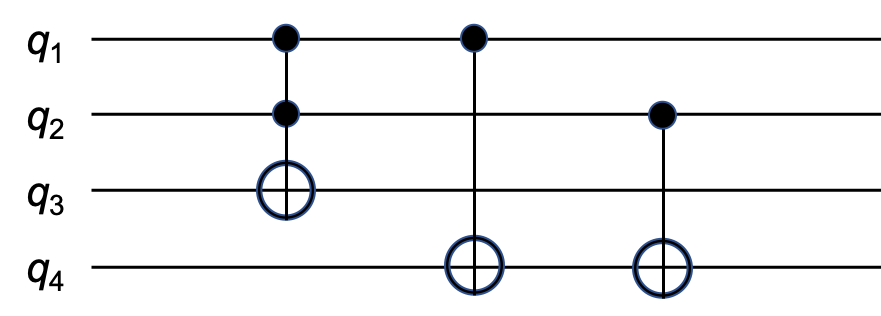
さて、\(q_1\) と \(q_2\) の足し算を実現し、結果を \(q_3\) と \(q_4\) に出力する操作は、
図に示すような\(q_1, q_2, q_3\) に対するCCNOTゲート操作と、
\(q_1, q_4\) に対するCNOTゲート操作、
\(q_2, q_4\) に対するCNOTゲート操作により実現されます。
ここで考えている4ビット系に対する上記のユニタリー変換は以下の行列によって表されます。
\begin{eqnarray}
U_{\rm CCNOT} =
\left(
\begin{array}{cccccccccccccccc}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0
\end{array}
\right),
\end{eqnarray}
\begin{eqnarray}
U_{\rm CNOT14} =
\left(
\begin{array}{cccccccccccccccc}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{array}
\right),
\end{eqnarray}
\begin{eqnarray}
U_{\rm CNOT24} =
\left(
\begin{array}{cccccccccccccccc}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{array}
\right)
\end{eqnarray}
4ビット系に対するユニタリー演算
よって、1+1の量子演算は、初期状態に対して上記ユニタリー変換を施した、
\[
v_{\rm fin} = U_{\rm CNOT24} U_{\rm CNOT14} U_{\rm CCNOT} v_{\rm ini}
\]
と表される。これは結果として
\[
v_{\rm fin}^{T} =
\left(
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0
\right),
\]
を与える。すなわち\(| 1110 \rangle\)状態へと変換されます。
この結果より、\( q_3 = 1, q_4 = 0 \)が計算結果として得られます。
つまり\(10\)が結果ですが、これは2進数で表されていますので、10進数では\(2\)に対応しますので、
1+1の計算結果が得られたことがわかります。
CCNOTとCCNOT
上記ではいきなりCNOTとCCNOT量子ゲートを導入しましたが、これらについて簡単に記します。
CNOTは2量子ビットに対してCCNOTは3量子ビットに対して以下の様に定義されます。
CNOTの回路図は

真理値表は
と表される。2ビット系に対するユニタリー変換行列は
\( |c, t \rangle = | 00 \rangle, | 01 \rangle, | 10 \rangle, | 11 \rangle
\)
の順に並ぶ基底に対して
\begin{eqnarray}
U_{\rm CCNOT(2bits)} =
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}
\right),
\end{eqnarray}
と表される。
一方、CCNOTの回路図は
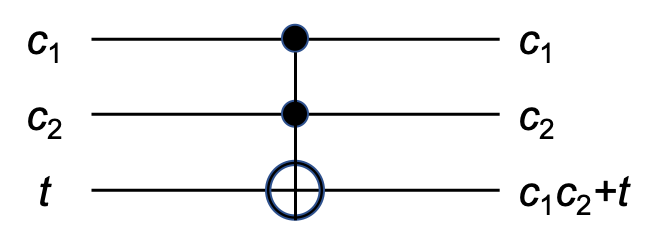
真理値表は
| \(c_1\) | \(c_2\) | \(t\) | \(c_1 c_2 + t\) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
と表される。3ビット系に対するユニタリー変換行列は
\( |c_1, c_2, t \rangle = | 000 \rangle, | 001 \rangle, | 010 \rangle, | 011 \rangle,
| 100 \rangle, | 101 \rangle, | 110 \rangle, | 111 \rangle
\)
の順に並ぶ基底に対して
\begin{eqnarray}
U_{\rm CNOT(3bits)} =
\left(
\begin{array}{cccccccc}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{array}
\right),
\end{eqnarray}
と表されます。
これらのユニタリー行列を4ビット系に拡張したものが上記のユニタリー行列になります。
なお最近では、シリコン量子ドットを用いた
CNOTゲート
や
CCNOTゲート(Toffoliゲート)
が報告されているようです。
以下では、\( q_1 + q_2 \) を実際に演算した結果がどのようになるのかを初期状態(ここでは\( q_1 q_2 0 0\) で指定します)に対して、上記ユニタリー変換を施すことによって試してみたいと思います。
入力: 出力:
Copyright © Wataru Izumida, All Rights Reserved.