4. 構造最適化¶
ここでは、構造最適化の方法について紹介します。 結晶構造は、３つの並進ベクトルで決まる単位胞と、単位胞内の原子座標で決定されるので、構造最適化には次のように3通りのパターンが考えられます。
単位胞のサイズを最適化する。
単位胞の形を固定したまま、原子の内部座標を最適化する。
単位胞の形と原子座標を両方最適化する。
以下でそれぞれの計算方法を紹介していきます。
4.1. 単位胞のサイズの最適化1¶
まず、結晶構造が与えられているときに、その格子定数の理論値を計算する方法をgrapheneを例にとって紹介します。
最も愚直にやる方法は、前の章で行った scf 計算を格子定数を変えて繰り返し行うことになります。 これにより、格子定数のエネルギー依存性をみることで最もエネルギーの低くなる格子定数を決める、ということができます。 まず graphene.scf.in とpseudopotential を用意した上で以下のようなスクリプトを用意して実行してみましょう。
#!/bin/bash
PWSCF=/usr/bin
for ((ia=-4; ia<=4; ia+=1)) do
#a=$(echo "scale=3; 4.600 + $ia/20.0" | bc -l)
a=$(echo $ia | awk '{printf ("%5.3f", 4.600 + $1/20.0)}')
echo $a
sed "s/4.602/$a/g" graphene.scf.in > graphene_${a}.scf.in
$PWSCF/pw.x < graphene_${a}.scf.in > graphene_${a}.scf.out
done
graphene_4.???.scf.out というファイルがいくつかできたと思います。 これが、各格子定数で scf計算を行った結果です。 格子定数とそのときのエネルギーを抜き出したファイルを作りましょう。
% grep "^\!" graphene_*.scf.out | sed "s/graphene_//g" | sed "s/.scf.*=//g" > etot.dat
% cat etot.dat
4.400 -22.82238911 Ry
4.450 -22.83358987 Ry
4.500 -22.84168131 Ry
4.550 -22.84687104 Ry
4.600 -22.84939047 Ry
4.650 -22.84945257 Ry
4.700 -22.84721331 Ry
4.750 -22.84287988 Ry
4.800 -22.83659433 Ry
これでエネルギーの格子定数依存性を計算した結果をファイルにまとめることができました。
あとは、これを適当なソフトでフィットしてやれば、格子定数の理論値が求まります。
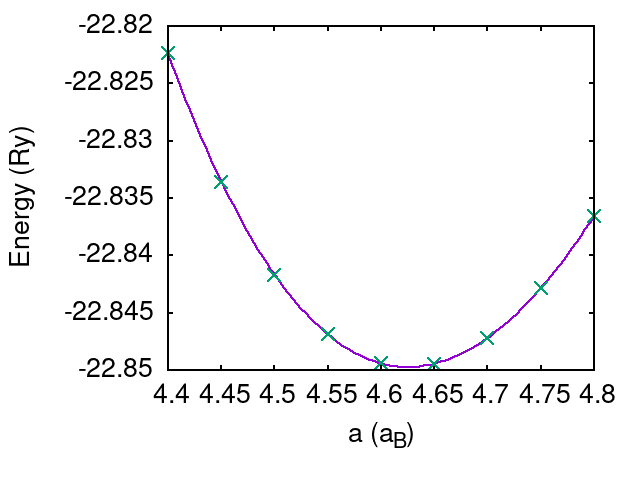
例えば gnuplot を使えば(fit.plt)、フィットした結果は以下の図のようになり、
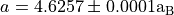という値が得られます。
4.2. 単位胞のサイズの最適化2¶
上記の方法だと、単位胞のサイズを決めるパラメータが複数ある場合、手で最適化するのは結構大変になります。 そこで次に、そのような場合にも使える方法として、calculation='vc-relax'を使った方法を graphite を例に紹介します。
以下のインプットファイル(graphite.vc-relax.in)を用意します。
&control
calculation = 'vc-relax'
prefix='graphite',
tstress = .true.
tprnfor = .true.
pseudo_dir = './',
outdir='./work/'
etot_conv_thr = 1.d-5
forc_conv_thr = 1.d-4
disk_io='low'
/
&system
ibrav = 4,
celldm(1) = 4.602,
celldm(3) = 3,
nat = 4,
ntyp = 1,
ecutwfc = 30.0,
ecutrho = 150.0,
occupations = 'smearing'
smearing = 'm-p'
degauss = 0.01
/
&electrons
mixing_beta = 0.7
conv_thr = 1.0d-8
/
&ions
/
&cell
/
ATOMIC_SPECIES
C 12.0107 C.pz-van_ak.UPF
ATOMIC_POSITIONS {crystal}
C 0.00 0.00 0.00
C 1/3 2/3 0.00
C 0.00 0.00 0.5
C 2/3 1/3 0.5
K_POINTS {automatic}
12 12 4 0 0 0
まず、
calculation = 'vc-relax'
とします。 vc-relax は単位胞と原子の内部座標を両方構造最適化するオプションですが、きれいな graphite 構造をつくれば炭素原子には力が働かないため、単位胞のサイズだけを最適化することができます。
&ions
/
&cell
/
構造最適化を行う際の単位胞と原子の運動に関するオプションを記述するところです。 default でも問題ないので何も記述していませんが、ないとエラーで終了してしまいますので、必ず入れて下さい。
&cell
press = 1000
/
のように圧力を指定することもできます。(この場合P=1000kbar=100GPaの元での構造最適化になります)
ATOMIC_POSITIONS {crystal}
C 0.00 0.00 0.00
C 1/3 2/3 0.00
C 0.00 0.00 0.5
C 2/3 1/3 0.5
グラファイトの構造を結晶の並進ベクトル a1, a2, a3 を単位として表しています。 座標としてこのように分数を使うこともできます。 ただし、これは最近の espresso でサポートされたものなので、XCrysden などの外部プログラムはサポートしていないことに注意して下さい。
これを以下のコマンドで実行します。
% pw.x < graphite.vc-relax.in > graphite.vc-relax.out
結果をみると以下のように出力されています。
bfgs converged in 13 scf cycles and 12 bfgs steps
(criteria: energy < 1.0E-05 Ry, force < 1.0E-04 Ry/Bohr, cell < 5.0E-01 kbar)
End of BFGS Geometry Optimization
Final enthalpy = -45.7064437393 Ry
File ./work/graphite.bfgs deleted, as requested
Begin final coordinates
new unit-cell volume = 231.46409 a.u.^3 ( 34.29944 Ang^3 )
density = 2.32590 g/cm^3
CELL_PARAMETERS (alat= 4.60200000)
1.004943736 -0.000000000 0.000000000
-0.502471868 0.870306805 0.000000000
0.000000000 0.000000000 2.715373964
ATOMIC_POSITIONS (crystal)
C 0.0000000000 0.0000000000 0.0000000000
C 0.3333333333 0.6666666667 -0.0000000000
C 0.0000000000 0.0000000000 0.5000000000
C 0.6666666667 0.3333333333 0.5000000000
End final coordinates
これをみれば、 a = 4.602*1.00494 = 4.625 (aB) = 2.45 (A), c = 4.602*2.71537 = 12.50 (aB) = 6.61 (A) という結果が得られ、 そのときのエンタルピー(E+PV)が -45.706 Ry であることが分かります。
vc-relax では、このあとこの構造でもう一度scf計算を行い、以下のような出力も得られます。
the Fermi energy is 7.0516 ev
! total energy = -45.70612066 Ry
estimated scf accuracy < 1.7E-11 Ry
smearing contrib. (-TS) = -0.00009503 Ry
internal energy E=F+TS = -45.70602563 Ry
The total energy is F=E-TS. E is the sum of the following terms:
one-electron contribution = -10.44158579 Ry
hartree contribution = 13.10912973 Ry
xc contribution = -13.93582327 Ry
ewald contribution = -34.43774630 Ry
convergence has been achieved in 8 iterations
Forces acting on atoms (cartesian axes, Ry/au):
atom 1 type 1 force = -0.00000000 -0.00000000 0.00000000
atom 2 type 1 force = 0.00000000 0.00000000 -0.00000000
atom 3 type 1 force = -0.00000000 0.00000000 -0.00000000
atom 4 type 1 force = -0.00000000 -0.00000000 0.00000000
Total force = 0.000000 Total SCF correction = 0.000000
Computing stress (Cartesian axis) and pressure
total stress (Ry/bohr**3) (kbar) P= -2.09
-0.00000971 0.00000000 0.00000000 -1.43 0.00 0.00
0.00000000 -0.00000971 -0.00000000 0.00 -1.43 -0.00
0.00000000 0.00000000 -0.00002320 0.00 0.00 -3.41
このように、最終構造でのエネルギーや、各原子にかかる力、セルにかかる圧力も計算されます。
注釈
この方法をそのまま graphene のインプットに適用するといつまで経っても収束しません。これは、c軸方向の長さも最適化しようとしてしまうからです。 c軸方向の長さを固定したまま vc-relax を行うには、以下のように &cell のブロックで cell_dofree = 'c'を指定します。
&cell
cell_dofree = 'c'
/
このように cell_dofree オプションを使えば、単位胞の一部のパラメータを固定したまま vc-relax を行うことができます。 cell_dofree で指定可能なオプションの詳細は INPUT_PW.html を参考にしてください。
4.3. 内部座標の最適化¶
次に bilayer graphene を例にして単位胞を固定した状態で内部構造を最適化する方法について紹介します。
面内の格子定数を固定して、グラフェンの計算と同様z方向が非常に大きな supercell をとり、層間距離は適当に決めたABスタックのbilayer graphene を置いた以下のようなインプットファイル(bilayer-graphene.relax.in)を用意します。
&control
calculation = 'relax'
prefix='graphene',
tstress = .true.
tprnfor = .true.
pseudo_dir = './',
outdir='./work/'
etot_conv_thr = 1.d-5
forc_conv_thr = 1.d-4
disk_io='low'
/
&system
ibrav = 4,
celldm(1) = 4.602,
celldm(3) = 6,
nat = 4,
ntyp = 1,
ecutwfc = 30.0,
ecutrho = 150.0,
occupations = 'smearing'
smearing = 'm-p'
degauss = 0.01
/
&electrons
mixing_beta = 0.7
conv_thr = 1.0d-8
/
&ions
/
ATOMIC_SPECIES
C 12.0107 C.pz-van_ak.UPF
ATOMIC_POSITIONS {crystal}
C 0.00 0.00 0.00
C 1/3 2/3 0.00
C 0.00 0.00 0.10
C 2/3 1/3 0.10
K_POINTS {automatic}
12 12 1 0 0 0
まず、計算のオプションとして
calculation = 'relax'
と指定します。 これで、単位胞固定のもとでの内部座標の最適化計算になります。
etot_conv_thr = 1.d-5
forc_conv_thr = 1.d-4
これは、relax 計算のときの収束条件を表します。 etot_conv_thr は1ステップ前と比べてエネルギーの変化がこれより小さくなっているかどうか、forc_conv_thr は原子に働く力がこれより小さくなっているか、という収束条件です。 default は etot_conv_thr = 1.d-4, forc_conv_thr = 1.d-3 で、単位はatomic unitです。 両方の条件を満たしたときに計算が終了します。
&ions
/
原子（イオン）の運動に関するオプションを記述するところです。
ATOMIC_POSITIONS {crystal}
C 0.00 0.00 0.00
C 1/3 2/3 0.00
C 0.00 0.00 0.10
C 2/3 1/3 0.10
面間距離は適当に決めてABスタックになるよう炭素を配置しました。
これを以下のコマンドで実行します。
% pw.x < bilayer-graphene.relax.in > bilayer-graphene.relax.out
bilayer-graphene.relax.out の最後の方に以下のような記述があれば計算完了です。
bfgs converged in 14 scf cycles and 12 bfgs steps
(criteria: energy < 1.0E-05 Ry, force < 1.0E-04 Ry/Bohr)
End of BFGS Geometry Optimization
Final energy = -45.7024689218 Ry
File ./work/graphene.bfgs deleted, as requested
Begin final coordinates
ATOMIC_POSITIONS (crystal)
C 0.0000000000 0.0000000000 -0.0630676784
C 0.3333333333 0.6666666667 -0.0631359480
C 0.0000000000 0.0000000000 0.1630676516
C 0.6666666667 0.3333333333 0.1631359748
End final coordinates
みて分かる通り、面内は全く変化せず面間距離が (0.163+0.063)*4.602*6 = 6.24 aB = 3.30 Aとなりました。
以下 relax 計算の注意点です。
default では relax のステップ数は50回で打ち切られることになっています。(オプション名はnstepです。vc-relaxも同様。) 従って、一見正常に終わっていても収束していないことがあるので注意してください。 出力をちゃんと読めば収束していないときはしていないと書いてあります。
relax の各ステップでは、ATOMIC_SPECIES で指定した質量と計算した力を用いて次のステップの座標を計算しています。 したがって、質量が重いとステップごとの変化が少なくなって収束が遅くなる場合があります。
relax は必ずしも最も安定な構造に落ち着くわけではありません。 複雑な構造の場合、いろいろな初期構造を試してみる必要があるかもしれません。 また、bilayer graphene のAAスタックのように対称性のよい配置から始めると、ABの方が安定であるにも関わらず、力が働かなくてAAのまま、ということになります。
一部の原子を固定して relax することもできます。固定する原子は座標の後ろに0 を３つ追加します。例えば
ATOMIC_POSITIONS {crystal} C 0.00 0.00 0.00 0 0 0 C 1/3 2/3 0.00 C 0.00 0.00 0.10 C 2/3 1/3 0.10
とすれば、原点にある炭素原子を固定して構造最適化できます。
4.4. 単位胞と内部座標の同時最適化¶
最後に単位胞と内部座標を同時に最適化する方法についてコメントします。 オプションは、単位胞のサイズの最適化2 で紹介した vc-relax になります。 vc-relax を使えば graphite のように原子にかかる力が完全にキャンセルされない限り、自動的に全て構造最適化されます。 従って、これを使えば scf 計算や relax 計算を使って構造最適化する必要はないと思われるかもしれません。 しかし、vc-relax は scf や relax に比べて、利用に際して注意することが多く、また計算がうまくいかずに終わってしまうこともあります。
具体的な vc-relax 利用上の注意点は以下の通りです。
vc-relax では、初期構造で計算に必要なパラメータを計算し、それらをずっとそのまま用いて最適化を行っていきます。 従って、最適化の前後で系のサイズが大きく変化する場合、最初に決めたパラメータが最適化後の構造では不適当であることがあります。 変化した後の構造を初期構造としてもう一度最適化してみるとよいでしょう。
単位胞にかかる力の計算には scf や relax での収束に必要なカットオフより、少し大きめのカットオフが必要になります。 どの程度のカットオフが必要かは scf 計算などの時とは別に吟味し直して下さい。
単位胞の変化に伴い、系の対称性が変化する場合があります。 default の計算だと系の対称性が変化したら、エラーを出して止まってしまいます。 その場合、初期構造を対称性が低いところからスタートする、あるいは、対称性を考慮しないオプション(nosym = .true.)を設定して計算を行って下さい。
原子の運動の速さは原子の質量で、単位胞の変化の速さは「単位胞の質量」(wmass)で決まります。 ステップごとの単位胞の体積変化が非常に小さい場合は wmass を小さくする、というように、これらの値を適切に設定することで収束を早めることができます。