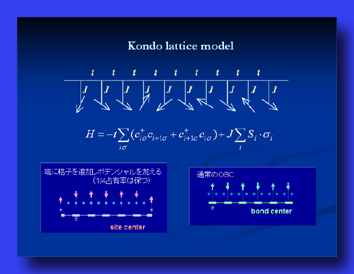
主な研究内容

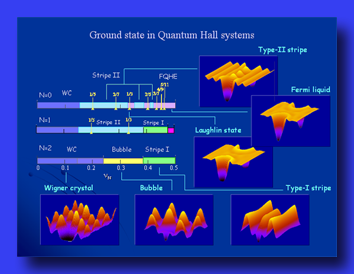
二次元電子系の基底状態（量子液体、電荷ストライプ、量子固体）

　物質中の電子を制御する技術の進歩は現代の工業製品の性能向上に大きな役割を果たしてきましたが、そこで制御の対象になり様々な機能を担っている実体は、半導体の界面に閉じ込められた２次元電子系です。この２次元電子系の状態を電場によって制御するのがトランジスタですが、そこに磁場を加えると、はるかに多彩な電子制御が可能になります。
　電子は磁場によってローレンツ力を受けます。そのため、磁場中ではサイクロトロン円運動が自発的に生じ、電子の軌道は閉じたループを形成するようになります。量子力学的に軌道が閉じるためには、軌道を一周回った後でその電子の波動関数の位相はもとに戻らなければならないので、その位相変化の大きさには制約が課せられます。波動関数の位相変化は運動量と関係するため、位相変化に課せられた制約は、電子の運動エネルギーを離散化させ、運動エネルギーは全てランダウ準位と呼ばれる特定の離散的な値に集約されます。
　このとき、同じランダウ準位に存在する電子は同じ運動エネルギーをもちますので、一般に全エネルギーが同じ電子配置が数多く現れ、基底状態には大きな縮退が出現します。これは、どのような電子配置で円運動を行っても、電子の運動エネルギーは常に同じになっていることを反映しています。
　このように、電子間相互作用がない場合には一般に膨大な数の縮退が磁場中の基底状態に現れますが、この縮退は電子間相互作用によって様々な形に解かれていきます。ここで特徴的なことは、運動エネルギーがすべて同じになっているため、相互作用によってのみ安定な電子配置が定まるということです。これは、磁場がないときの状況との大きな違いであり、このように相互作用によって大きな縮退が一気に解かれることで形成される電子状態は、円運動する電子の波動関数の形や平均電子間距離に依存してさまざまな状態に変化し、その結果、量子液体、電荷ストライプ、量子固体といった強相関電子系の特徴ともいえる多彩な量子多体状態が形成されます。
　このような系の性質を正しく理解するためには、電子間相互作用によって生じる量子多体問題を、摂動論のような近似理論を使用せずに解くことが求められます。本研究室では、そのような問題に対する最も優れた計算法として知られる数値的解析法（DMRG)を利用しており、これまでの計算法では難しかった二次元量子多体系の基底状態の相図の決定や、実験的に得られている分数量子ホール効果や異方的電気抵抗、リエントラント整数量子ホール効果などの様々な現象の解明を行っています。

重い電子系（スピン液体、磁気秩序、電荷秩序）

　　磁性や超伝導など物質の示す基本的性質を理解するためには多くの場合電子間の相互作用の効果の解明が必要です。この電子間相互作用を取り扱う問題は量子多体問題と呼ばれ、物質の性質をミクロな立場から理解する際には避けることのできない難問として存在しています。この問題に特に焦点が当てられている研究対象が重い電子系や高温超伝導です。重い電子系には非常に局在した軌道をとる電子が存在し、それらの電子の間には強い原子内クーロン相互作用が働きます。このクーロン相互作用が多体効果の起源となりますが、重い電子系の場合にはさらに結晶内を遍歴する伝導電子が存在し、空間的に広がったそれらの電子は局在電子と異なる強い波動性をもっています。そのため重い電子系では性格の異なる電子が共存することになり、電子間の多体効果に加え、局在性と遍歴性という量子力学の基本概念を反映した多彩な現象が現れます。本研究室では、このような電子系に見られる多様な物性の研究も行っています。