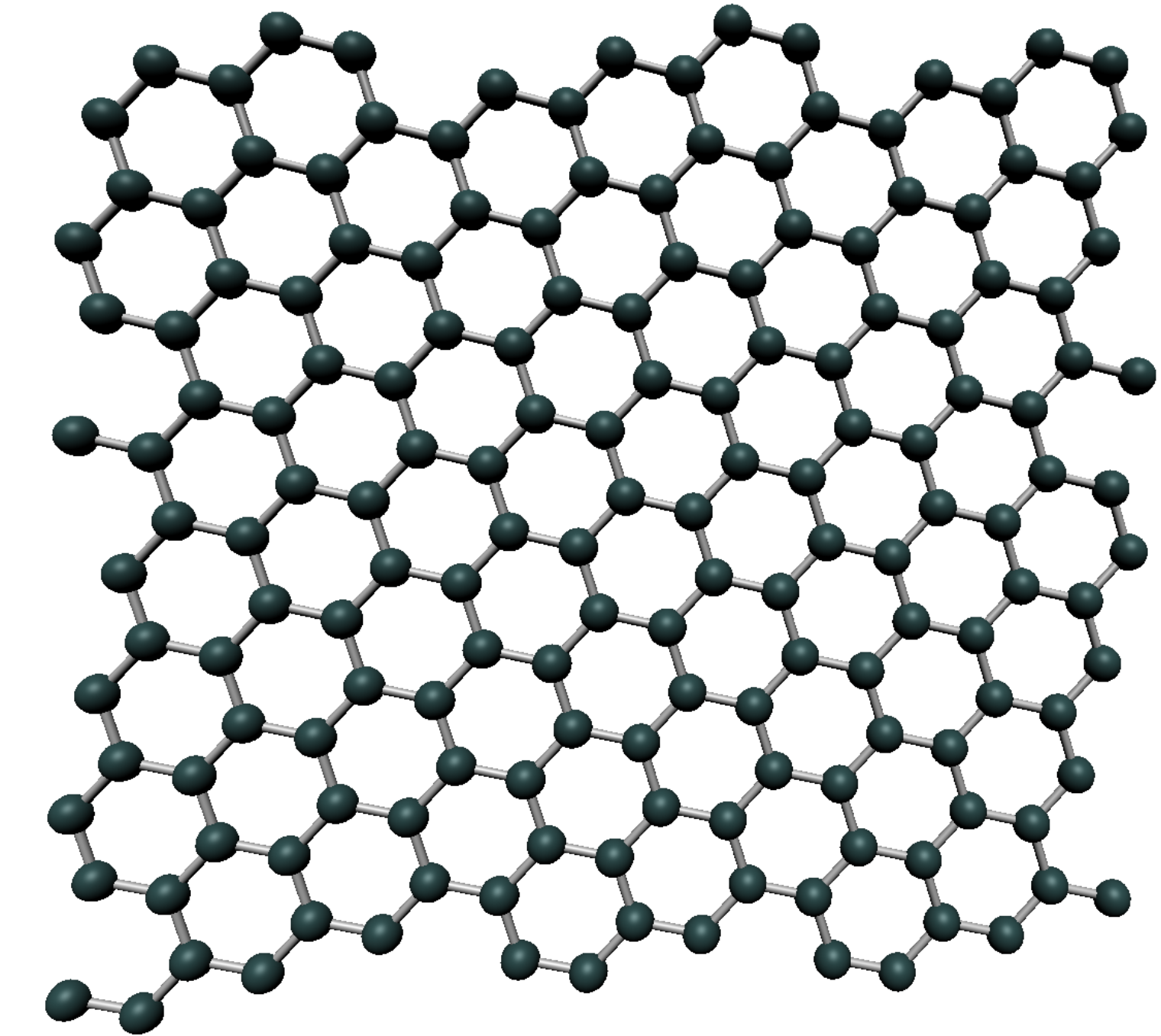
カーボンナノチューブとは、炭素のみで構成された円筒状の物質である。
その円筒表面はハニカム状の格子で構成され、2次元物質であるグラフェンと同じ構造を持つ。
カーボンナノチューブの結晶構造はカイラルベクトル \[ \mathbf{C_h} = n\mathbf{a_1} + m\mathbf{a_2} \] によって決まる。ただし、\(\mathbf{a_1}\), \(\mathbf{a_2}\) はグラフェンの基本格子ベクトル、\(n, m\) は任意の整数である。
ナノチューブは軸方向に対して並進対称性を有する。軸方向の並進ベクトル \(\mathbf{T}\) は \[ \mathbf{T} = t_1 \mathbf{a_1} + t_2 \mathbf{a_2} \] で与えられる。ここで、\(t_1, t_2\) は互いに素な整数であり、\(\mathbf{T} \cdot \mathbf{C_h} = 0\) を満たすため \[ t_1 = \frac{2m + n}{d_R}, \quad t_2 = -\frac{2n + m}{d_R} \] となる。
チューブの単位胞は \(\mathbf{C_h}, \mathbf{T}\) で囲まれる長方形から構成される。単位胞の面積を六角形の面積で割ると、 \[ N = \frac{|\mathbf{C_h} \times \mathbf{T}|}{|\mathbf{a_1} \times \mathbf{a_2}|} = \frac{2(n^2 + m^2 + nm)}{\sqrt{3}a^2 / d_R} \] となる。グラフェンの単位胞には2つの炭素原子があるため、ナノチューブ単位胞内の原子数は \(2N\) 個である。
グラフェンのタイトバインディングハミルトニアンは \[ H = -t \sum_{\mathbf{r}} \sum_{j=1}^3 \left( |\mathbf{r}_A \rangle \langle \mathbf{r}_B + \boldsymbol{\delta}_j| \right) + \text{H.c.} \] と表される。
波動関数を \[ |\mathbf{k} \rangle = \frac{1}{\sqrt{N}} \sum_{j=1}^N e^{i \mathbf{k} \cdot \mathbf{r}_j} |\mathbf{r}_j \rangle \] としたとき、エネルギーは次のように与えられる： \[ \langle A\mathbf{k} | H | B\mathbf{k} \rangle = t \sum_{j=1}^3 e^{i\mathbf{k} \cdot \mathbf{\delta_j}} \]
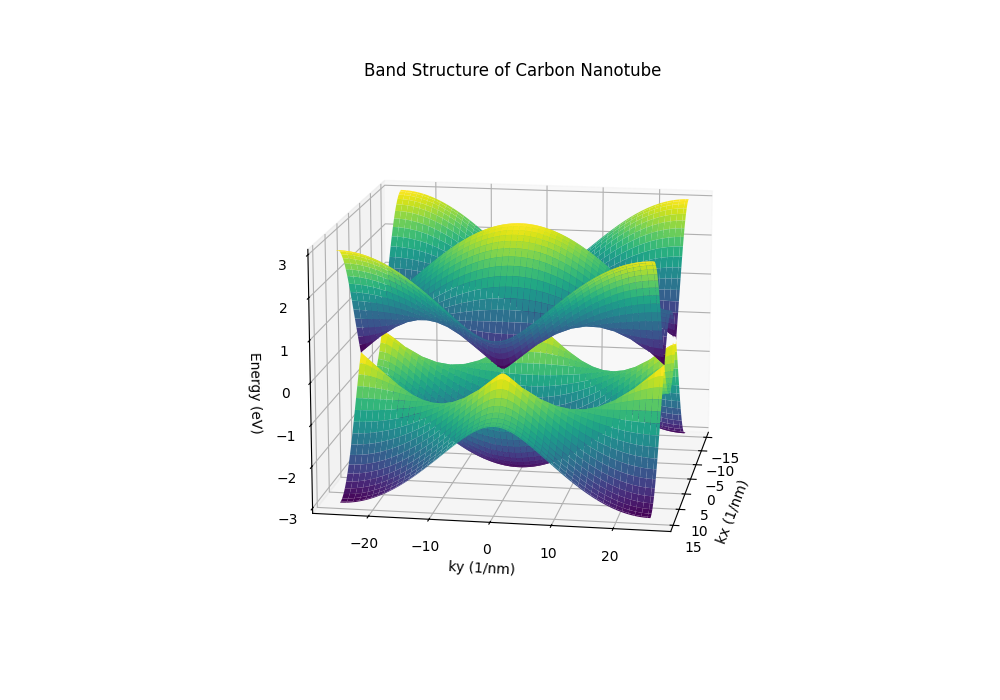
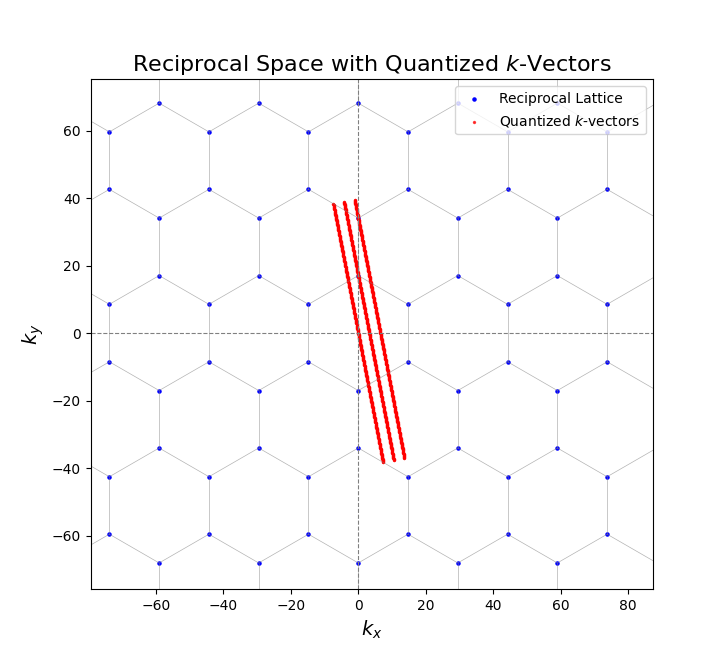
単層カーボンナノチューブの電子状態は、円周方向 \(\mathbf{C_h}\) を量子化することで得られる。 周期境界条件により \(\mathbf{K}_1\) 方向の波数が量子化され、それぞれに対して軸方向 \(\mathbf{T}\) の波数 \(k\) を持つ一次元バンドが形成される。 これをカッティングラインと呼び、 \[ \mathbf{k} = \mu \mathbf{K}_1 + k \frac{\mathbf{K}_2}{|\mathbf{K}_2|} \] と表される。
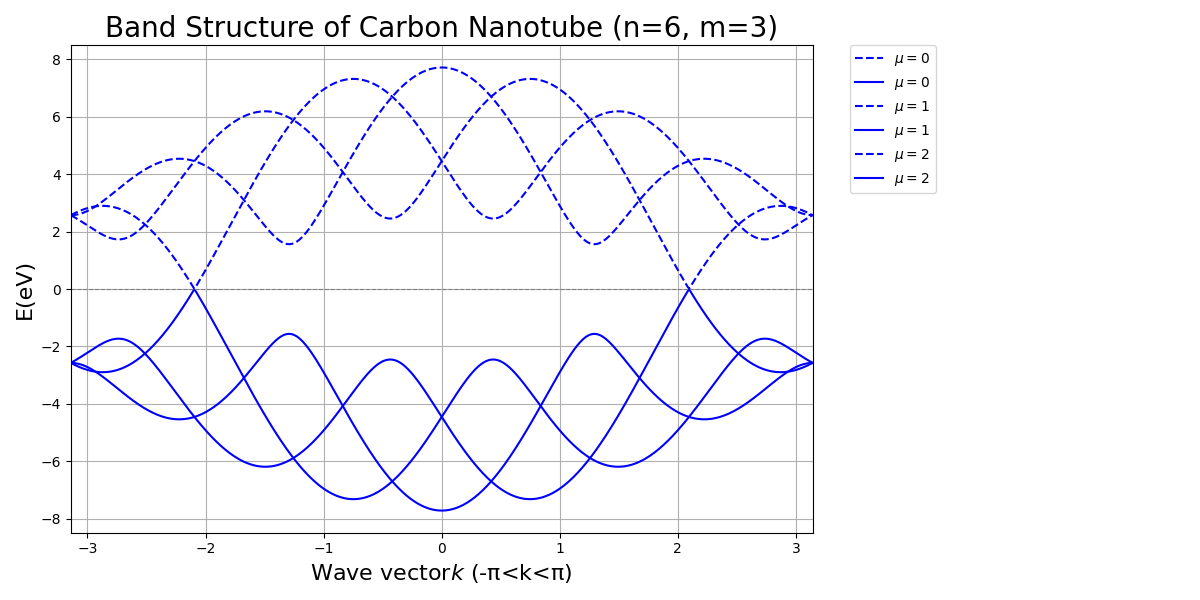
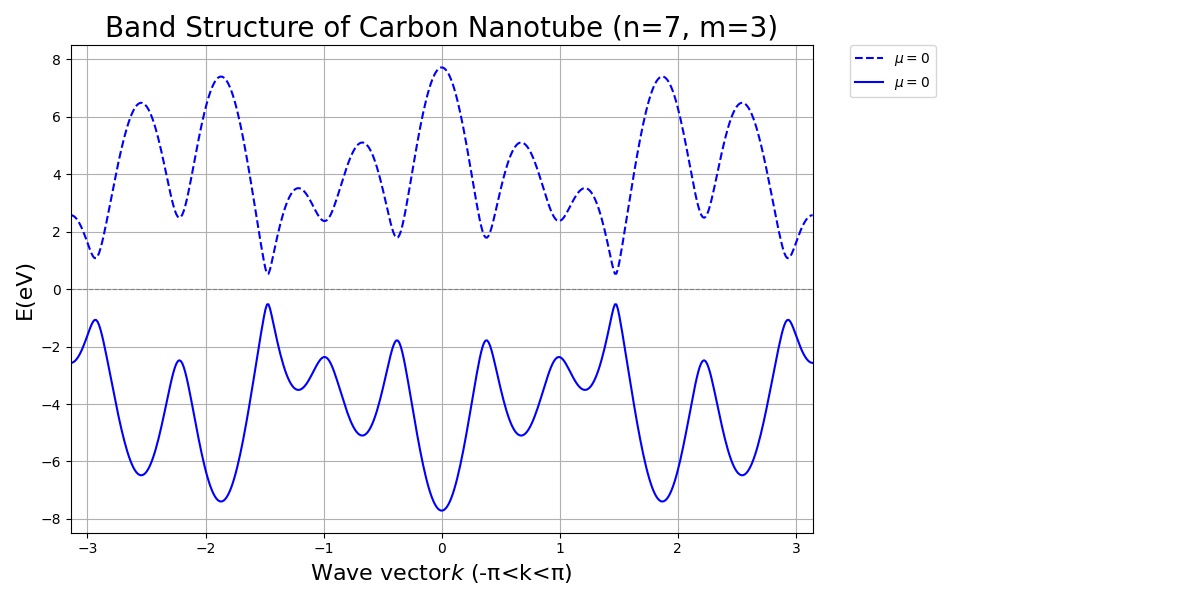
原子数 \(2N\) により \(N\) 個の \(\pi\) バンドと \(\pi^*\) バンドが存在し、カッティングラインが \(\mathbf{K}\) 点を通る場合は金属、通らない場合は半導体となる。
波数空間において、六員環の中点を\(\mathbf{\Gamma}\)とすると、\(\mathbf{K}\)までのベクトル\( \mathbf{\Gamma K}\)は \[ \mathbf{\Gamma K} = \frac{1}{3}(-\mathbf{b}_1 + \mathbf{b}_2) = -\frac{n - m}{3} \mathbf{K}_1 + \frac{t_1 - t_2}{3} \mathbf{K}_2 \]
\( \mathbf{\Gamma K}\)が整数の場合、cutting lineはK点、K'点を通りCNTのエネルギーバンドはディラック点で交差する。
\( \mathbf{\Gamma K}\)が整数でない場合、cutting lineはK点、K'点を通らずCNTのエネルギーバンドはギャップが生じる。
よって、CNTは\(\text{mod}(n - m, 3) = 0\) のとき金属となり、それ以外は半導体である。 半導体の場合のエネルギーギャップは \[ E_g \approx \frac{4\hbar v_F}{3d_t} \] となり、1eV程度になる。
実際にpythonを用いて数値計算を行うと、以下の図が得られる。
