Tight-Banding model
Tight-Banding modelは、バンド計算の際に用いられる近似の一つである。
系の波動関数を、各原子座標における孤立原子に対する波動関数の重ね合わせにより近似 $
今、1次元(鎖状)に原子がN個並んでいるとする。このとき電子が原子位置jにおける最近 $
このとき、電子の状態を表す波数ベクトル\(|k\rangle\)は
\[
|k\rangle = \frac{1}{\sqrt{N}}\sum_{j}^N e^{ikj} |j\rangle
\]
と与えられる。このときの電子のハミルトニアン\(H\)は
\[
H = -t\sum_{j}(|j\rangle \langle j+1|) + \mathrm{H.c.}
\]
ただしH.c.はエルミート共役
だから、これを対角化すると、この1次元格子の電子のエネルギーは、
\[
\langle k| H |k \rangle = \frac{1}{N}\sum_{j,j'}^N e^{ik(j'-j)} \langle j|H|j'\rangle \]
\(\langle j| H |j' \rangle\ = t \delta_{j,j+1} + t \delta_{j,j-1}\)だから、
\[
\langle k| H |k \rangle = -t[e^{ik} + e^{-ik}]
\]
\[
= -2t cos (k)
\]
これにより、1次元鎖モデルのエネルギーを近似的に求めることができる。
実際にpythonを用いて数値計算を行うと、以下の図が得られる。
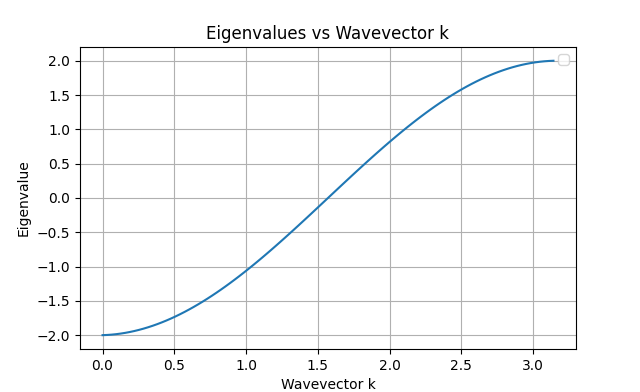 図1: 1次元鎖モデルのエネルギーバンド
図1: 1次元鎖モデルのエネルギーバンド

