tetrahedron法について

tetrahedron法とは、離散的なk点上で得られた物理量からk空間の積分値を求めるときに使われる手法です。 具体的に、状態密度の計算を例にとって見てみましょう。 状態密度D(E)の定義は

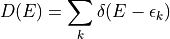
D(E) = \sum_k \delta(E - \epsilon_k)

で与えられます。 しかし、離散的なk点に対して、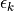\epsilon_k が分かっているとき単純にこの式を使うとデルタ関数が有限個あるだけの非現実的な状態密度になってしまいます。 最も簡単にこの問題を回避するには、

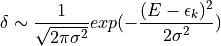
\delta \sim \frac{1}{\sqrt{2\pi\sigma^2}} exp( -\frac{(E - \epsilon_k)^2}{2\sigma^2})

のようにデルタ関数をガウシアンで近似することだと思います。実際 k点のメッシュ間隔を細かくとり、それに合わせて適切なσを選んでやればそこそこまともな近似になるでしょう。(occupations='smearing' のままで計算すれば、この方法での状態密度が得られます。degauss の値がσに対応します。) しかし、van Hove singularity などはかなり鈍ってしまいますし、バンドギャップの値もσの分小さくみえてしまうなど、あまりきれいな状態密度が得られるとは言い難いでしょう。

この問題を回避するのが tetrahedron法です。

まず簡単のため1次元系を考えてみます。 離散的なk点に対して 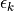\epsilon_k が与えられているとき、連続的なkに対する 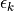\epsilon_k の近似として最も簡単なものは離散的な k点の間を直線で内挿することです。 この近似的な:math:epsilon_k' を使って解析的にD(E)の積分を実行してやれば、D(E)としては階段関数が得られます。 この方法を用いると、メッシュを細かくしていけば、ガウシアンを使う場合よりも早く確実にD(E)に近づいていきますし、ギャップは離散的なメッシュ上でのギャップ値がそのまま反映されます。 これがtetrahedron法の一次元版です。

3次元にこの方法を拡張するには、3次元上で同様な線形な内挿をしてやればよいことになります。 しかし、立方体の中をそのまま線形に内挿することはできません。 そこで、立方体をさらに６つの四面体(tetrahedron)に分割してやります。(これが tetrahedron法の名前の由来です。) すると、それぞれの四面体の中では、線形な内挿が可能になります。 こうして、各四面体内で内挿した:math:epsilon_k を使って解析的にD(E)を積分してやれば、tetrahedron法による状態密度が得られることになります。

詳細は Bloch et al. などをご覧下さい。