2. グラフェンのバンド構造と状態密度¶
まず、簡単な計算例として、グラフェンのバンド構造と状態密度を求めてみましょう。 どちらも scf計算->non-scf計算->後処理という流れになります。
2.1. scf計算¶
何を計算するにしても、まず scf 計算により電荷密度(charge density)を求める必要があります。 scf 計算に必要なファイルはインプットファイル graphene.scf.in は以下の通りです。 とりあえずこのファイルをダウンロードして、適当な directory において下さい。
&control
calculation = 'scf'
prefix='graphene',
tstress = .true.
tprnfor = .true.
pseudo_dir = './',
outdir='./work/'
disk_io='low'
wf_collect=.true.
/
&system
ibrav = 4,
celldm(1) = 4.602,
celldm(3) = 4,
nat = 2,
ntyp = 1,
ecutwfc = 30.0,
ecutrho = 150.0,
occupations = 'smearing'
smearing = 'm-p'
degauss = 0.01
/
&electrons
mixing_beta = 0.7
conv_thr = 1.0d-8
/
ATOMIC_SPECIES
C 12.0107 C.pz-van_ak.UPF
ATOMIC_POSITIONS {crystal}
C 0.00 0.00 0.00
C 0.33333333 0.66666667 0.00
K_POINTS {automatic}
12 12 1 0 0 0
特に重要なパラメータは以下の通りです。
単位胞の構造
ibrav = 4, celldm(1) = 4.602, celldm(3) = 4,
hexagonal 構造(ibrav=4)をもち、
a1 = a(1,0,0), a2 = a(-1/2,sqrt(3)/2,0), a3 = a(0,0,c/a)
としたときの a=4.602 (単位はボーア半径:aB, 1A~0.529177aB), c/a=4 としています。
元素の種類と原子数
nat = 2, ntyp = 1,
炭素1種類(ntyp=1)で、単位胞内の原子数は2(nat=2)
原子位置
ATOMIC_POSITIONS {crystal} C 0.00 0.00 0.00 C 0.33333333 0.66666667 0.00
格子ベクトルa1, a2, a3を単位として(crystal)原子位置を指定。
0*a1 + 0*a2 + 0*a3, 1/3*a1 + 2/3*a2 + 0*a3
の2点におくと、graphene ができあがる。
カットオフエネルギー
ecutwfc = 30.0, ecutrho = 150.0,
ecutwfc は波動関数を平面波で展開するときのカットオフエネルギー。単位は Ry。ecutrho は電荷密度を展開するときのカットオフ。 ノルム保存の擬ポテンシャルを使っていれば ecutrho は自動的に ecutrho = 4*ecutwfc となるため設定しなくてよいが、ウルトラソフトの場合は 4*ecutwfc より 大きめにとったほうがよい。
k点の取り方
K_POINTS {automatic} 12 12 1 0 0 0
12x12x1 のk点をとることを表してます。0 0 0 はメッシュを全体的にシフトさせるかどうかで、今の場合Γ点を含むメッシュになっています。 12 12 1 1 1 0 なら、メッシュの中央にΓ点がきます。
pseudopotential
C 12.0107 C.pz-van_ak.UPF
炭素に対して pseudopotential のファイル C.pz-van_ak.UPF を使うことを意味しています。 これは、quantum ESPRESSO の website からダウンロードできるファイルの一つです。 pseudopotential の内容については、このファイルの先頭に簡単な記述がありますが、C.pz-van_ak.UPF は Perdew-Zunger のパラメータを用いたLDAを使った ultrasoft型の pseudopotential になっています。 12.0107 は炭素の質量ですが、この計算では利用しません。
注釈
ここでは、炭素のpseudopotentialとしてこのファイルを用いますが、炭素に対してこの pseudopotential の使用を推奨しているわけではないのでご注意下さい。 pseudopotential の選択(作成)は計算しようとしている物理量や計算量にも関係してくるため、その都度吟味する必要があります。
以上の内容は第一原理計算を行っている論文なら大抵記載されており、これでほぼ計算の内容は決まります。
各パラメータの意味の詳細は INPUT_PW.html を参照して下さい。
注釈
ここで設定したパラメータ以外にも非常に多くのパラメータが設定できます。 この計算では default の値で問題ないので省略していますが、本格的に計算する場合は INPUT_PW.html を一読しておくことをお勧めします。
計算を流すためにはさらに pseudopotentialのファイル C.pz-van_ak.upf を pseudo_dirで設定しているディレクトリに置く必要があります。 今の場合、pseudo_dir = './' ですので current directory に C.pz-van_ak.UPF を置いて下さい。 この状態で以下のコマンドを実行すれば scf計算が行われます。
% pw.x < graphene.scf.in > graphene.scf.out
結果は、graphene.scf.out に出力されます。このファイルをみて最後の方に
the Fermi energy is -0.4659 ev
! total energy = -22.84944327 Ry
estimated scf accuracy < 7.5E-10 Ry
smearing contrib. (-TS) = -0.00007836 Ry
internal energy E=F+TS = -22.84936491 Ry
The total energy is F=E-TS. E is the sum of the following terms:
one-electron contribution = -89.64895244 Ry
hartree contribution = 46.53456839 Ry
xc contribution = -6.97846974 Ry
ewald contribution = 27.24348888 Ry
convergence has been achieved in 6 iterations
とあればうまく計算ができています。
なお、この計算によって得られるグラフェンのエネルギーは
% grep -a "^\!" graphene.scf.out
とすればコマンドラインからも確認できます。
2.2. band計算¶
次に、scf で計算した charge density を用いて任意のk点に対するKohn-Sham軌道のエネルギーを計算します。 scf計算に利用した graphene.scf.in から以下のハイライトした行だけ変更した graphene.nscf.in というファイルを作成してください。
&control
calculation = 'bands'
prefix='graphene',
tstress = .true.
tprnfor = .true.
pseudo_dir = './',
outdir='./work/'
disk_io='low'
wf_collect=.true.
/
&system
ibrav = 4,
celldm(1) = 4.602,
celldm(3) = 4,
nat = 2,
ntyp = 1,
ecutwfc = 30.0,
ecutrho = 150.0,
occupations = 'smearing'
smearing = 'm-p'
degauss = 0.01
nbnd = 16
/
&electrons
mixing_beta = 0.7
conv_thr = 1.0d-8
/
ATOMIC_SPECIES
C 12.0107 C.pz-van_ak.UPF
ATOMIC_POSITIONS {crystal}
C 0.00 0.00 0.00
C 0.33333333 0.66666667 0.00
K_POINTS {tpiba_b}
4
0.00000000 0.00000000 0.00000000 30
0.66666667 0.00000000 0.00000000 30
0.50000000 0.28867500 0.00000000 30
0.00000000 0.00000000 0.00000000 30
nbnd の行は計算するバンド数の指定で、指定しなくても構いません。(デフォルトの値については INPUT_PW.html を参照してください。)
最後の5行で、Γ(0,0,0)-K(2/3,0,0)-M(1/2,1/2sqrt(3),0)-Γのライン上に各30点ずつ計算するよう指定しています。 tpiba_b はこの座標指定に 2pi/a を単位として用いることを表しています。 代わりにcrystal_b を指定すれば以下のように逆格子ベクトル単位で指定することもできます。
K_POINTS {crystal_b}
4
0.00000000 0.00000000 0.00000000 30
0.66666667 -0.33333333 0.00000000 30
0.50000000 0.00000000 0.00000000 30
0.00000000 0.00000000 0.00000000 30
また、ibrav を0以外にしている場合は
K_POINTS {crystal_b}
4
gG 30
K 30
M 30
gG 30
のようにk点の位置をシンボルで表すこともできます。(今の場合、ibrav = 4 を指定しているので、 gG はΓ点、KはK点と解釈されます。) この表記方法の詳細はespressoを展開したディレクトリの中にある、Doc/brillouin_zones.pdfを参照してください。
このファイルを scf計算した directory と同じところにおいて
% pw.x < graphene.nscf.in > graphene.nscf.out
とやればバンド計算終了です。
あとは、計算したKohn-Shamエネルギーをファイルにまとめます。それ専用のプログラム bands.x があるので、以下のようなインプットファイル graphene.band.in を用意します。
&bands
outdir = './work/',
prefix='graphene',
filband='graphene.band',
lsym=.true.
/
このファイルを用いて以下のコマンドを実行します。
% bands.x < graphene.band.in > graphene.band.out
これで、graphene.band および graphene.band.gnu というファイルができるはずです。
注釈
Mac でgfortranを使ってコンパイルした場合、エラーで落ちてしまうかもしれません。 そのときはこちらの インプット を試してみて下さい。
graphene.band というファイルには、以下のように各k点ごとにKohn-Shamエネルギーのリストが出力されています。
&plot nbnd= 16, nks= 91 /
0.000000 0.000000 0.000000
-20.113 -8.374 -3.513 -3.513 2.628 4.431 5.452 8.033 8.033 10.527
11.344 12.549 13.122 19.981 22.155 23.138
0.022222 0.000000 0.000000
-20.104 -8.363 -3.549 -3.533 2.640 4.443 5.464 8.039 8.073 10.538
11.312 12.561 13.136 19.988 22.186 23.149
0.044444 0.000000 0.000000
-20.078 -8.331 -3.656 -3.593 2.677 4.479 5.500 8.057 8.189 10.572
11.217 12.597 13.176 20.008 22.274 23.183
0.066667 0.000000 0.000000
-20.033 -8.277 -3.827 -3.693 2.738 4.540 5.560 8.087 8.375 10.629
11.060 12.658 13.246 20.040 22.417 23.240
0.088889 0.000000 0.000000
-19.971 -8.201 -4.056 -3.829 2.823 4.624 5.644 8.132 8.620 10.708
10.845 12.743 13.347 20.080 22.606 23.324
0.111111 0.000000 0.000000
-19.891 -8.104 -4.335 -4.001 2.932 4.732 5.752 8.191 8.909 10.576
10.809 12.851 13.485 20.124 22.827 23.439
0.133333 0.000000 0.000000
-19.794 -7.986 -4.653 -4.206 3.066 4.864 5.884 8.266 9.229 10.258
...
また、graphene.band.gnu というファイルには gnuplot でプロットしやすいよう加工されたデータが出力されます。
これを gnuplot で band.plt というファイルを使ってプロットします。(この辺は人によってそれぞれ流儀があるところだと思います。あくまで参考程度に。)
% gnuplot band.plt
これで、次のようなファイルが生成されます。
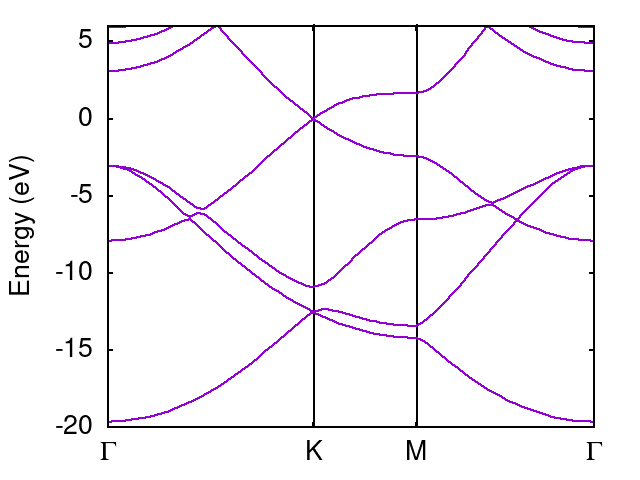
注釈
このプロットでは、E=0がFermi energyになるようにエネルギーをシフトしています。 (もともとの出力におけるエネルギー原点には意味がないので、普通、Fermi energy あるいは valence top などをエネルギー原点に なるようシフトしてプロットします。)
Fermi energy は graphene.scf.out に出力されていますが、あくまで離散的なk点を使って推測したものになります。 今の場合、厳密に K点のエネルギーを用いればいいと分かっているので、そちらを優先しています。
2.3. DOS計算¶
次に状態密度を求めてみましょう。
バンド計算したディレクトリとは別のディレクトリで、scf 計算を行って下さい。
% pw.x < graphene.scf.in > graphene.scf.out
その後、scf計算に利用した graphene.scf.in から以下のハイライトした行だけ変更した graphene.nscf.in というファイルを作成してください。
&control
calculation = 'nscf'
prefix='graphene',
tstress = .true.
tprnfor = .true.
pseudo_dir = './',
outdir='./work/'
disk_io='low'
wf_collect=.true.
/
&system
ibrav = 4,
celldm(1) = 4.602,
celldm(3) = 4,
nat = 2,
ntyp = 1,
ecutwfc = 30.0,
ecutrho = 150.0,
occupations = 'tetrahedra'
/
&electrons
mixing_beta = 0.7
conv_thr = 1.0d-8
/
ATOMIC_SPECIES
C 12.0107 C.pz-van_ak.UPF
ATOMIC_POSITIONS {crystal}
C 0.00 0.00 0.00
C 0.33333333 0.66666667 0.00
K_POINTS {automatic}
36 36 1 0 0 0
最後の2行で、36x36x1 のメッシュ状のk点を計算するよう指定しています。 実際には対称性を用いて計算するk点の数を減らしています。 また、occupationsとしてtetrahedron法を用いるように指定しています。 tetrahedron法の詳細については、 tetrahedron法について をご覧下さい。 第一原理計算に限らず、限られたk点メッシュの情報からk空間での積分の近似計算を行う上で非常に有用な手法です。
このファイルを用いて nscf 計算を行います。
% pw.x < graphene.nscf.in > graphene.nscf.out
あとは、計算したエネルギーをまとめてDOSの計算を行います。 専用のプログラム dos.x のインプットとして、以下のようなファイル graphene.dos.in を用意します。
&dos
outdir = './work/',
prefix='graphene',
fildos='graphene.dos',
/
このファイルを用いて dos.x を実行すると、
% dos.x < graphene.dos.in > graphene.dos.out
graphene.dos というファイルができるはずです。 これはそのままプロットすれば以下のような図が得られます。
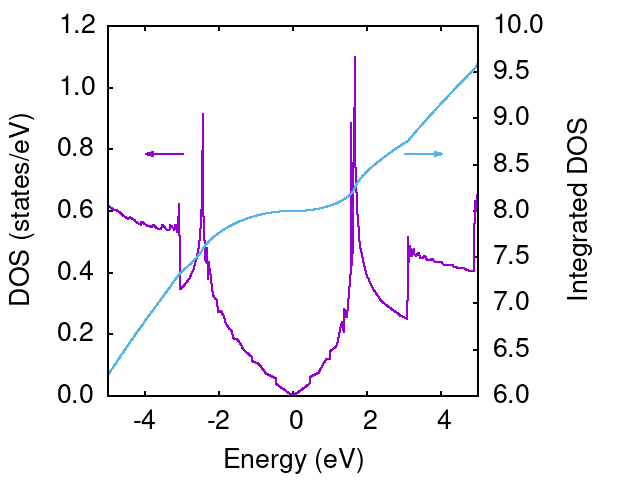
E=0はFermi energyで、Dirac点に対応しており、DOSが0になります(紫線)。 一方、DOSの積分(青線)は電子数に対応しており、E=0の値が8になっているのはEF以下に8個電子があることを意味しています。 これは、単位胞に2つ炭素原子があり、それぞれ4つずつ電子を考えていることに対応しています。(1sの電子は擬ポテンシャルの中に入っているため、炭素あたり2s,2pに4つ電子がいると考えている)